如果你曾經聽過一個物理學家提到“宇宙的邊緣”,那么他一般是指“可見宇宙的邊緣”。最遠處射來的光大致來自于150億年前。然而,通過一項精細的關于宇宙膨脹的研究,我們可以測得那些光源如今距離我們已有450億光年。如果你定義可見宇宙的大小為當前的物理距離(以“共動坐標”在宇宙微波背景中靜止為依據)到我們能看見的最遠物體,那么可見宇宙的邊緣就大約有450億光年遠。然而,從本質上來說,“邊緣”是一種視野,只是決定了你能夠看多遠而已。

當然,你也許會問:“那我們到底能夠看多遠呢?”大部分人對于宇宙的印象為宇宙被包裹在某種氣泡之中,所以導致他們本身會認為宇宙就是有邊緣的。但是,如果假設宇宙確實有邊界,那么將會有不少疑問。

如果你認為宇宙突然終止于一個邊緣,那么你必須指出粒子和它是如何相互作用的。顯然,我們不能夠繼續向前,只能彈開或者停止,但這都違背了動量守恒和能量守恒的原理。此外,如果你認為時空在一個確切的地方有一個確切的邊緣,那就違背了相對論等價(即任何物體在所有地點和速度下都是一樣的)。也許相對論會被質疑是否有例外的可能性,但是數學就沒有那么容易被反駁了。

理論認為宇宙是完全沒有邊界的。有以下三種情況:
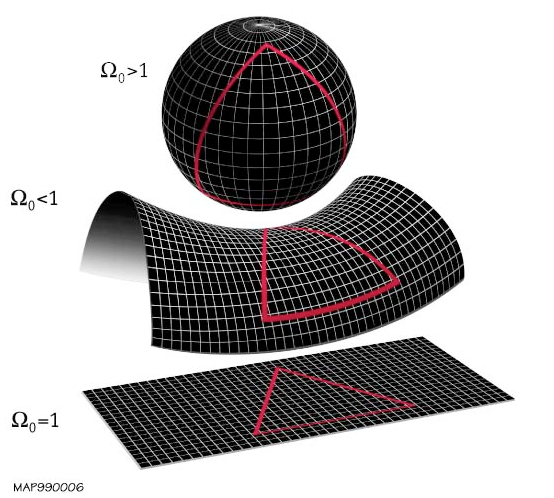
宇宙形狀的三種可能選項。
1)一個負彎曲的無限宇宙。這種情況已被一個關于宇宙微波背景分布的研究排除。
2)一個扁平的無限宇宙(沒有任何彎曲)。迄今為止的測量(天文愛好者也許已經知道該怎么測量了)都表明宇宙是扁平的,或是近乎扁平。但是,無垠的宇宙讓大家都有些不安。一個無限宇宙會將可見宇宙中的一切重復無限次,包括所有可能的細小的變化和所有完全不同的變化。拋開這個想法不談,真正令物理學家們困擾的是一個無限宇宙(近乎同質)會包含無數的物體與能量。并且,宇宙大爆炸(假設其真的發生過)會在任何地方發生。那么無數的宇宙大爆炸將會比傳統意義上的其數字描述來得更為糟糕。
3)一個彎曲的有限宇宙。這是最佳的一種情況。你可以想象宇宙是一個四維球體表面的一個三維空間。同樣的可以這樣理解,一個氣球的表面就是一個被三維球體包圍的二維空間。這樣的話就直接導致了這么一個問題:球體的里面是什么?要解答這個問題,我們不能忘記定義一個空間的,是其內部的物體如何相互關聯的(唯一能夠定義空間的是標尺)。

所以,即使你把氣球里面的那一面外翻,還是只能得到相同的空間。或者,如果你不擅長處理拓撲關系,那就別忘了空間外是不存在任何東西的,四維球體的表面就是空間。但是請注意,“四維球體的三維表面”這樣的描述不是完全確切的。假設我們不生活在三維,而是三加一維(不是空間,而是時空),那它的度量標準就會變得有些不能理解。同樣的,當你談論到“宇宙的形狀”時,一般是指“當下宇宙的形狀”。遺憾的是,“當下”這個概念在宇宙中并不被廣泛認可,因為宇宙中存在著循環的物體。所以說,“一個球體的表面”仍是描述宇宙的最好方法。

鑒于我們最好的測量顯示宇宙是非常扁平的,如果宇宙確實如第三種情況所述,是一個彎曲的有限宇宙(很有可能是),那么它將會非常非常大。這就如同你可以簡單地觀察到一個球體是有曲面的,但是很難觀察到地球也是有曲面的。
最后,回答一下最初的問題:宇宙是沒有邊緣的。
參考資料
1.WJ百科全書
2.天文學名詞
3. The Physicist- askamathematician
如有相關內容侵權,請于三十日以內聯系作者刪除
轉載還請取得授權,并注意保持完整性和注明出處
 酷播亮新聞
酷播亮新聞